辐射度量学概念辨析

Radiant energy

$Q$

$[J = Joule]$

The energy of electromagnetic radiation

Radiant flux

$\phi \equiv \frac{dQ}{dt} $

$[W = Watt] [lm = lumen]$

Energy per unit time

Radiant intensity

$I(\omega) \equiv \frac{d\phi}{d\omega}$

$[cd = candela = \frac{lm}{sr}]$

Radiant flux per unit solid angle

思考：Radiant intensity主要用于描述光源的性质，对于一个均匀点光源，空间内任意一点的Radiant intensity应当是相等的，且等于点光源功率 $\phi$ 除以 $4\pi$ 。

Irradiance

$E(x) \equiv \frac{d\phi(x)}{dA}$

$[lux = \frac{lm}{m^2}]$

The flux per unit area incident on a surface point.

思考：Irradiance 总是对于平面上一点而言的，而不是对于某条光线而言的。

Radiance

$L(p, \omega) \equiv \frac{d^2\phi(p, \omega)}{d\omega dA \cos\theta}$

$[nit = \frac{cd}{m^2} = \frac{lm}{sr \space m^2}]$

The flux emitted, reflected, transmitted or received by a surface, per unit solid angle, per projected unit area.

思考：Radiance 是对于某个方向上的一条光线而言的。

Irradiance定义中cosθ的理解

如下图所示，初始笔记中的理解还是有所偏差，红色小字为具体修正部分。

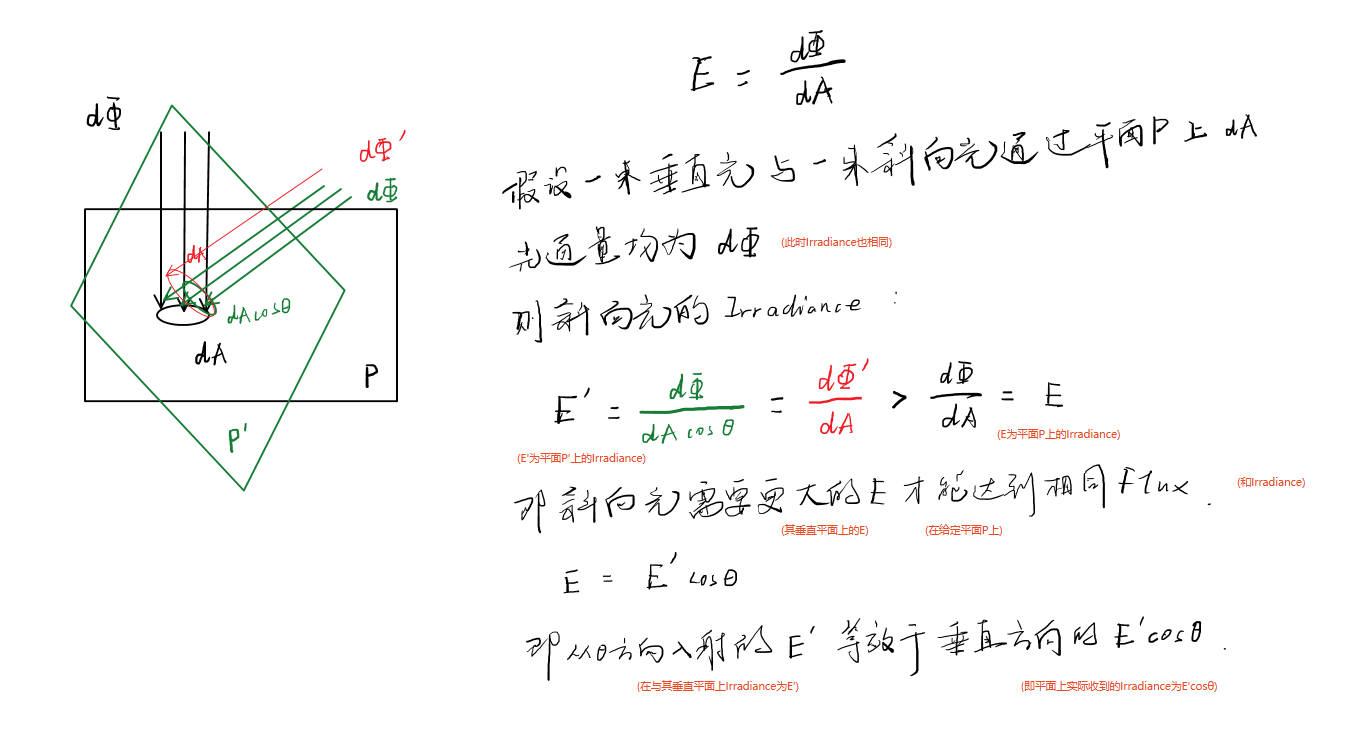
引入 $\cos\theta$ 的本质原因是在计算入射 $Irradiance$ 时，一束光线照射在倾斜平面$P$上面积$dA$的光通量 $d\phi$ 实际上是其垂直平面$P’$上通过面积$dA$的光通量 $d\phi’$ 的 $\cos\theta$ 倍。即导致了 $E=E’\cos\theta$ ，其中 $E’$ 为该光线在垂直平面上造成的 $Irradiance$ 。

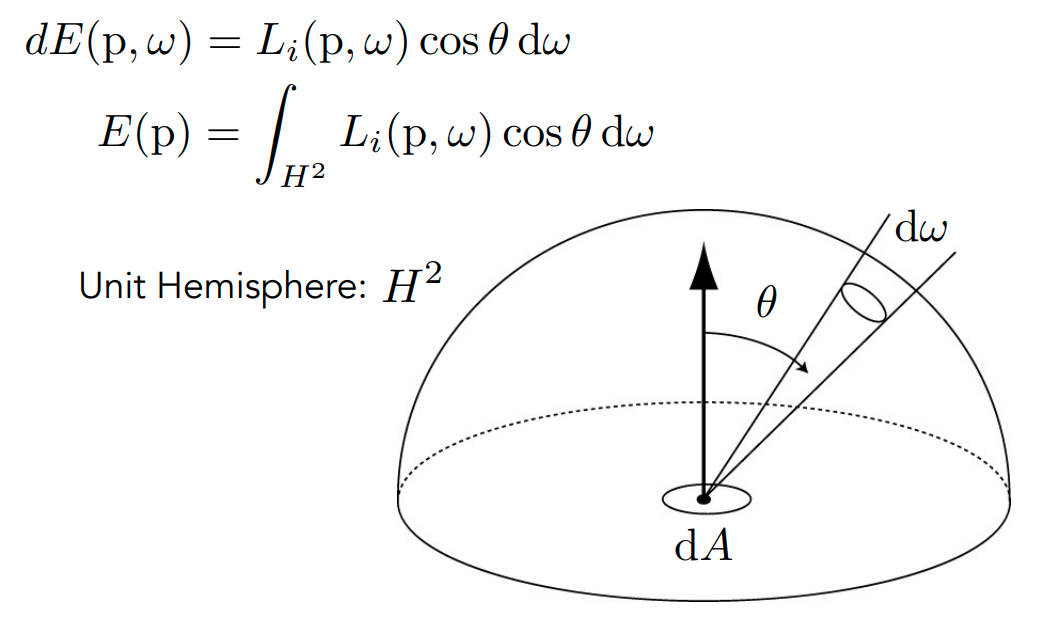
而由于 $Radiance$ 描述的是光线的性质，所以始终为其垂直平面上的 $\frac{dE}{d\omega}$ ，当其照射在倾斜平面上 $dA$ 时，$L(p, \omega) \equiv \frac{d^2\phi(p, \omega)}{d\omega dA_\perp}\equiv \frac{d^2\phi(p, \omega)}{d\omega dA \cos\theta}$

渲染方程简化

首先，渲染方程为：

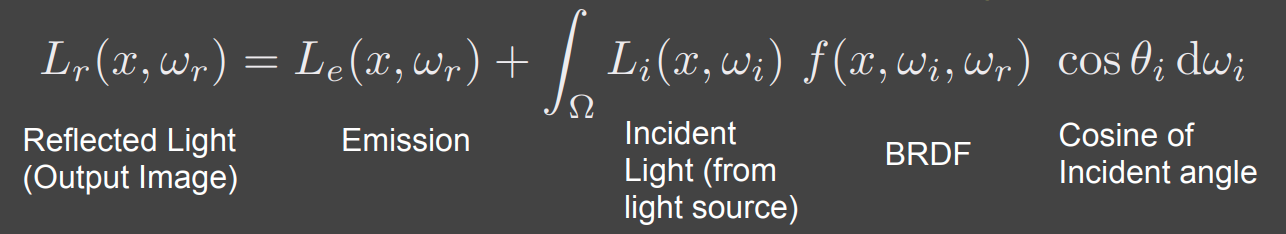
将对于 $x$ 的入射光 $L_i$ 替换为从另一物体 $x’$ 发出的反射光（包括其自发光）：

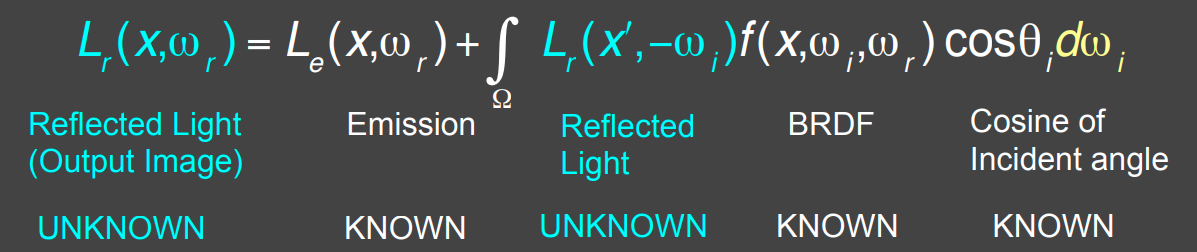
进一步，将BRDF的反射计算简化为一个算子，用 $K$ 表示：

对于全局而言，一个物体的 $l(u)$ 会在另一个物体的式子中充当 $l(v)$，所以可以将全局所有的光照计算写成一个矩阵方程形式：

当场景中有 $a,b,c$ 三个物体时，可以简单理解为：
$$
\left[
\begin{matrix}
a_o \\
b_o \\
c_o
\end{matrix}
\right]

\left[
\begin{matrix}
a_e \\
b_e \\
c_e
\end{matrix}
\right]
+
K_{3\times3}
\left[
\begin{matrix}
a_o \\
b_o \\
c_o
\end{matrix}
\right]
$$
其中：
$$
K=
\left[
\begin{matrix}
0 & k_{ba} & k_{ca} \\
k_{ab} & 0 & k_{cb} \\
k_{ac} & k_{bc} & 0
\end{matrix}
\right]
$$

Russian Roulette方法中运用的思想

在Path tracing中，理论上光线需要递归弹射无数次，我们无论怎样设置截断次数都将得到一个理论上不正确的值。

使用Russian Roulette可以非常巧妙的解决这一问题：对于一次光线弹射，设定以概率 $P$ 打出光线并计算结果，而概率 $1-P$ 不打出光线。将打出光线的计算结果除以 $P$ ，则其期望为理论正确值 $L_o$ 。对一次弹射而言这种处理毫无意义且引入误差，而对于多次计算则大不相同，对于同一条光线多次多层递归计算后的结果求期望，其结果依概率收敛于光线进行无穷次弹射的正确值。

对于一束光线，需要计算 $n$ 次弹射的概率为 $P^n$ ，随 $n$ 的增大而趋于零，这使得该递归算法总能终止。 $P$ 越小时算法终止越快，性能越好，计算结果随机误差越大；$P=1$ 时相当于原始思路，光线将会弹射无数次，递归算法无法终止。

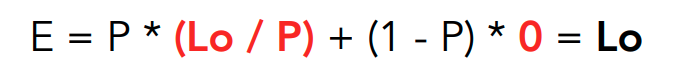
这一方法成功将截断误差消除在是否打出光线的随机性中，系统误差化为随机误差，从而得到了正确无偏的值。

太妙了，总感觉这个思路将来可以用于解决其他问题。

重要性采样的目的

蒙特卡洛积分中，可以使用均匀采样和重要性采样。两种采样方式的积分结果期望是相同的，均随样本量的增加收敛于真实值，也就是说两种采样方式都是正确而无偏的。所以，重要性采样的目的在于，在同样的采样数下有效减少积分结果的方差，即积分结果更加收敛于真实值。

Lambert Diffuse BRDF 推导

设BRDF为 $f_r(\omega_i, \omega_o)$
$$
f_r(\omega_i, \omega_o) = \frac {dL_o}{dE_i} = \frac {dL_o}{L_i\cos\theta_id\omega_i}
$$
则入射光 $L_i$ 在 $\omega_o$ 方向上的反射光为：
$$
dL_o = f_r(\omega_i, \omega_o)L_i\cos\theta_id\omega_i
$$
在半球面上反射的 $dE_o$ 为：
$$
dE_o = \int_\Omega dL_o\cos\theta_od\omega_o
\
=\int_\Omega(f_r(\omega_i, \omega_o)L_i\cos\theta_id\omega_i)\cos\theta_od\omega_o
\
=L_i\cos\theta_id\omega_i\int_\Omega f_r(\omega_i, \omega_o)\cos\theta_od\omega_o
$$
由能量守恒有：
$$
dE_o \le dE_i = L_i\cos\theta_id\omega_i
$$
即
$$
\int_\Omega f_r(\omega_i, \omega_o)\cos\theta_od\omega_o \le 1
$$
由于Lambert Diffuse的BDRF与方向无关，应为常数$C$，设反射率为 $\alpha\le1$，则有：
$$
\int_\Omega C\cos\theta_od\omega_o = \alpha
$$
计算球面积分，解得：
$$
f_r(\omega_i, \omega_o) = C = \frac\alpha\pi
$$